Cours de maths : les fonctions polynômes du second degré

Cet article s'adresse aux élèves en première et qui suivent la spé maths. Il est consacré aux polynômes du second degré qui intervient de façon majeure dans la résolution d'équations et inéquations algébriques et dans l'étude des fonctions.

POINT 1 : Présentation générale et vocabulaire

• On appelle fonction polynôme du second degré, toute fonction f définie sur ℝ par :

f(x) = ax²+bx+c, où a, b et c sont des nombres réels avec a non nul.

• On appelle racine du polynôme f, toute solution de l'équation f(x) =0 ; c'est-à-dire tout nombre réel α tel que f(α) = 0.
• L'écriture f(x) = ax²+bx+c est appelée la forme développée et réduite du polynôme f.

Nos profs de maths

Nicola 1^er cours offert (1)10100

Jean 1^er cours offert (22)9100

Un petit exemple : Considérons la fonction polynôme f définie par f(x) = 2x²+x - 3. Vérifier que 1 est une racine du polynôme f.

On a f(1) = 2(1)²+1 - 3 =2+1-3=0. Donc 1 est bien une racine de f.

Considérons un polynôme du second degré f qui s'écrit f(x) = ax²+bx+c sous la forme développée réduite. Alors :

• f peut s'écrire de façon unique sous la forme :

f(x) = a(x-α)²+β, où α et β sont des nombres réels. Cette écriture est appelée la forme canonique du polynôme f.

• Si de plus, le réel  β est non nul et de signe contraire de celui de a, le polynôme f peut alors aussi s'écrire sous la forme :

f(x) = a(x – x₁)(x – x₂), où x₁ et x₂ sont des nombres réels qui sont alors les racines de f. Cette écriture est appelée la forme factorisée du polynôme f.

Prendre des cours particuliers de maths

REMARQUE : En fonction du problème à résoudre, on peut passer d'une forme (développée réduite, canonique ou factorisée) à l'autre comme on l'illustre dans le récapitulatif ci-dessous.

Un exemple : Considérons la fonction polynôme f définie par f(x) = 2x²+x - 3. Établir la forme canonique du polynôme f puis le factoriser.

Voici maintenant un récapitulatif des différentes écritures d'un polynôme du second degré que nous venons d'introduire.

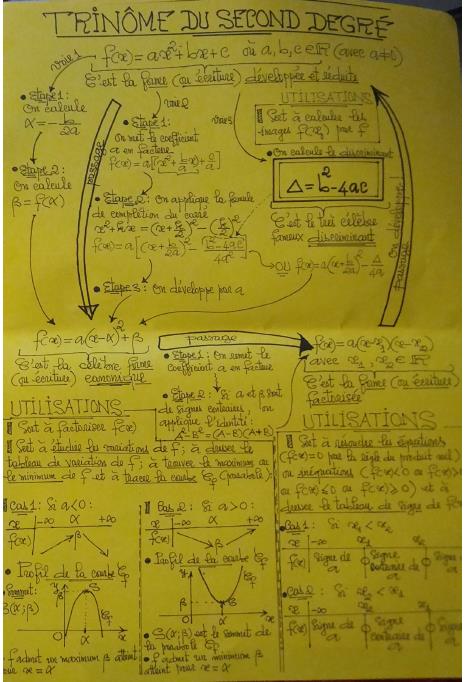
POINT 2 : Racines, factorisation et signe d'un polynôme du second degré

Nous allons énoncer le théorème fondamental concernant les polynômes du second degré. Mais commençons par un petit exercice.

Un petit exercice : 1) Considérons la fonction polynôme f définie par f(x) = 3x²- 4x +1.

a) Établir la forme canonique du polynôme f puis le factoriser.

b) Dresser le tableau de signe de la fonction f.

2) Prouver que pour tout (x ; y)∊ℝ², on a x²- xy + y²≥0.

Le théorème particulièrement important que tout le monde attend est le suivant :

REMARQUE : Ce théorème qui donne les racines d'un polynôme du second degré, est une conséquence de la forme canonique qui s'écrit aussi directement :

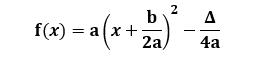
On est souvent amenés à déterminer le signe d'une expression faisant intervenir des polynômes du second degré. On dispose alors du très précieux théorème suivant qui donne aisément le signe d'un polynôme du second degré et qui joue un rôle majeur dans l'étude des fonctions.

UTILISATION : Ce théorème permet de résoudre des inéquations du second degré.

Retrouvez la suite de ce cours de maths dans une partie 2.