Cours de maths : calculer l'aire d'un triangle

On a tous eu un cours de maths sur le calcul d'aire des figures de base (carré, rectangle, triangle, cercle ...) au primaire.

En particulier, lorsqu'on vous demande de calculer l'aire d'un triangle, vous connaissez probablement tous la formule : S = b.h / 2 (où b est la base et h est la hauteur). Mais saviez-vous d'où sort cette formule ?

Dans cet article je vais vous expliquer pourquoi ce calcul nous donne bien l'aire d'un triangle.

Nos profs de maths

Nicola 1^er cours offert (1)10100

Jean 1^er cours offert (22)9100

Première idée

Commençons par visualiser ce schéma :

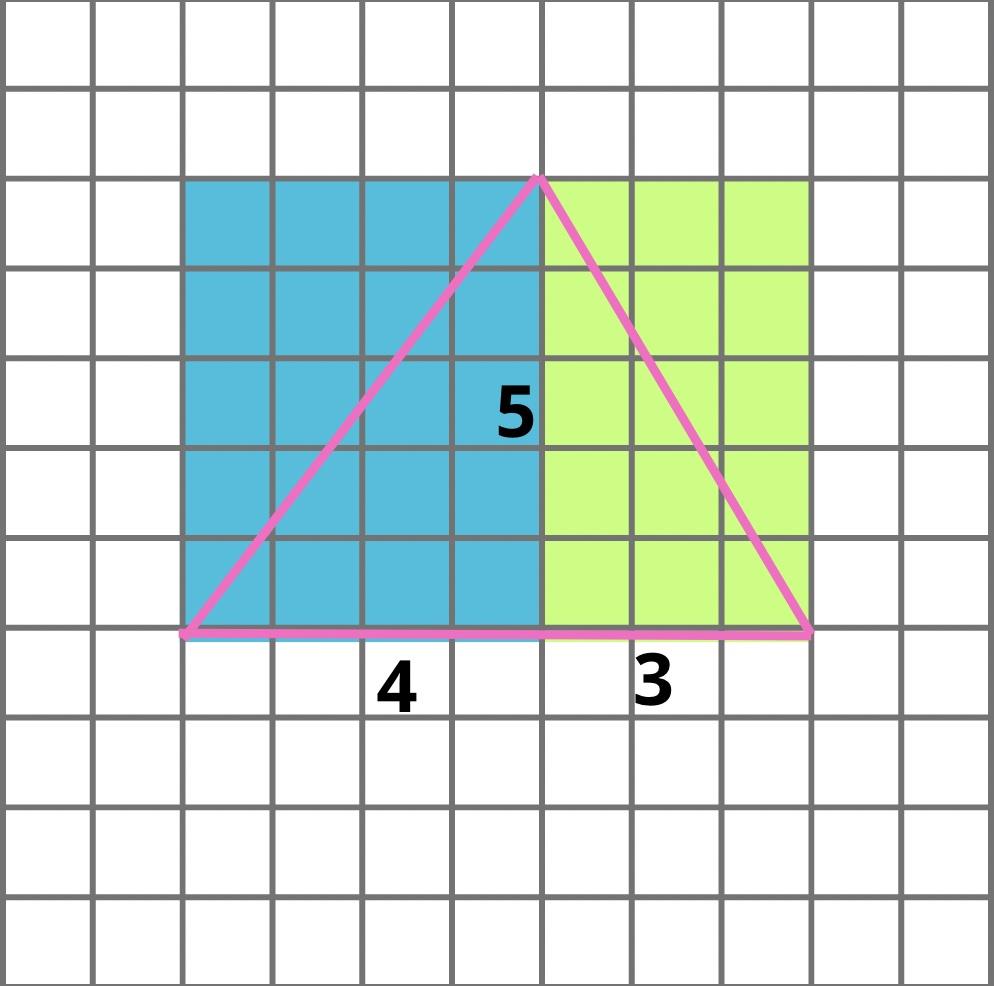
On considère le triangle rose. On veut calculer son aire.
La formule nous dit qu'il faut multiplier la base par la hauteur et diviser le tout par deux.
Faisons ceci :

• Base = 4 + 3 = 7
• Hauteur = 5
• Donc S = (7x5) / 2 = 35 / 2 = 17,5

Maintenant, regardons le problème sous un autre angle. Comme sur la figure, découpons le triangle rose en 2 triangles : bleu et vert. Pour chacun de ces deux triangles, complétons le triangle pour trouver un rectangle. On obtient donc un rectangle vert et un rectangle bleu, et la surface de chacun des deux vaut le double de la surface des triangles.

On a : 

• Aire du triangle rose = aire du triangle vert + Aire du triangle bleu

Or : 

• Aire du triangle vert = moitié de l'aire du rectangle vert

Et :

• Aire du triangle bleu = moitié de l'aire du rectangle bleu

Donc :     

• Aire du triangle vert + aire du triangle bleu = moitié (rectangle vert + rectangle bleu)

On connaît l'aire des rectangles, il suffit de multiplier la longueur par la largeur.

On a donc :

• Aire du rectangle vert = 3 x 5 = 15
• Aire du rectangle bleu = 4 x 5 = 20

Alors : 

• Moitié (rectangle vert + rectangle bleu)
  = 1/2 x (15+20)
  = 1/2 x 35 
  = 17,5

On retrouve bien le fameux 17.5, étant la surface du triangle rose qu'on a trouvé par la formule du début. On a bien vérifié, alors, que cette dernière est correcte !

Cours de maths en ligne

Deuxième idée

Une autre façon de le voir est la suivante.

On considère la figure ci-dessous :

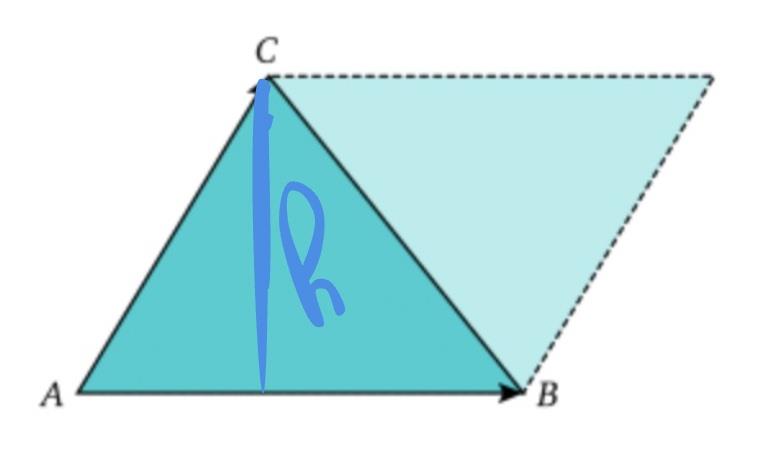
On voit bien que si on copie le triangle ABC, qu'on le colle juste à côté avec une petite rotation, on obtient un parallélogramme.

On a donc :

• Aire du parallélogramme = 2 x aire du triangle

Ou encore :

• Aire du triangle ABC = 1/2 x aire du parallélogramme.

Observons aussi que le triangle ABC et le parallélogramme ont la même hauteur h et la même base : AB ! À partir de ces deux remarques, essayons de faire les calculs par les deux méthodes :

Méthode 1 : en utilisant la formule

• S = ( b x h ) / 2
• S= ( AB x h ) / 2

Méthode 2 : avec l'idée du parallélogramme

• S = 1/2 x ( aire du parallélogramme )
• S = 1/2 x ( base x hauteur)
• S = 1/2 x (AB x h)

On retrouve bien le même résultat avec les deux méthodes.

À noter que selon votre niveau d'études, il y a d'autres formules qui permettent de calculer l'aire d'un triangle. On cite par exemple celle-ci :

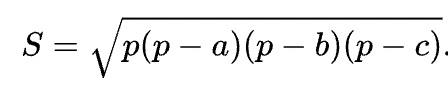
Où p est le demi périmètre et a, b, c sont les longeurs de côtés. 

Vérifions que cette formule soit bien valable.

On considère le triangle ABC qui a comme côté :

• AB = 3 cm ; AC = 4 cm ; AC = 5cm

Ce triangle est rectangle en A (vous pouvez le vérifier avec le théorème de Pythagore).

Son aire est donc : S = (3x4)/2 = 12/2 = 6

Prendre des cours particuliers

Vérifions si notre formule fonctionne :

Le demi-périmètre vaut : p = (3+4+5)/2 = 12/2 = 6

En appliquant la formule, on trouve donc :

• S = racine carré de (6x(6-3)x(6-4)x(6-5)) 
• = racine carrée de (6 x 3 x 2 x 1)
• = racine carrée de 36
• = 6

On retrouve bien le résultat.

Cette formule s'appelle la formule de Héron, Héron étant un mathématicien grec.