- Blog
- Mathematiques
- Quelques informations sur le théorème d...
Quelques informations sur le théorème de Pythagore, les triangles rectangles, les cercles
La dissection
Visualisez le grand carré : son aire est égale à la somme des aires des deux petits carrés.
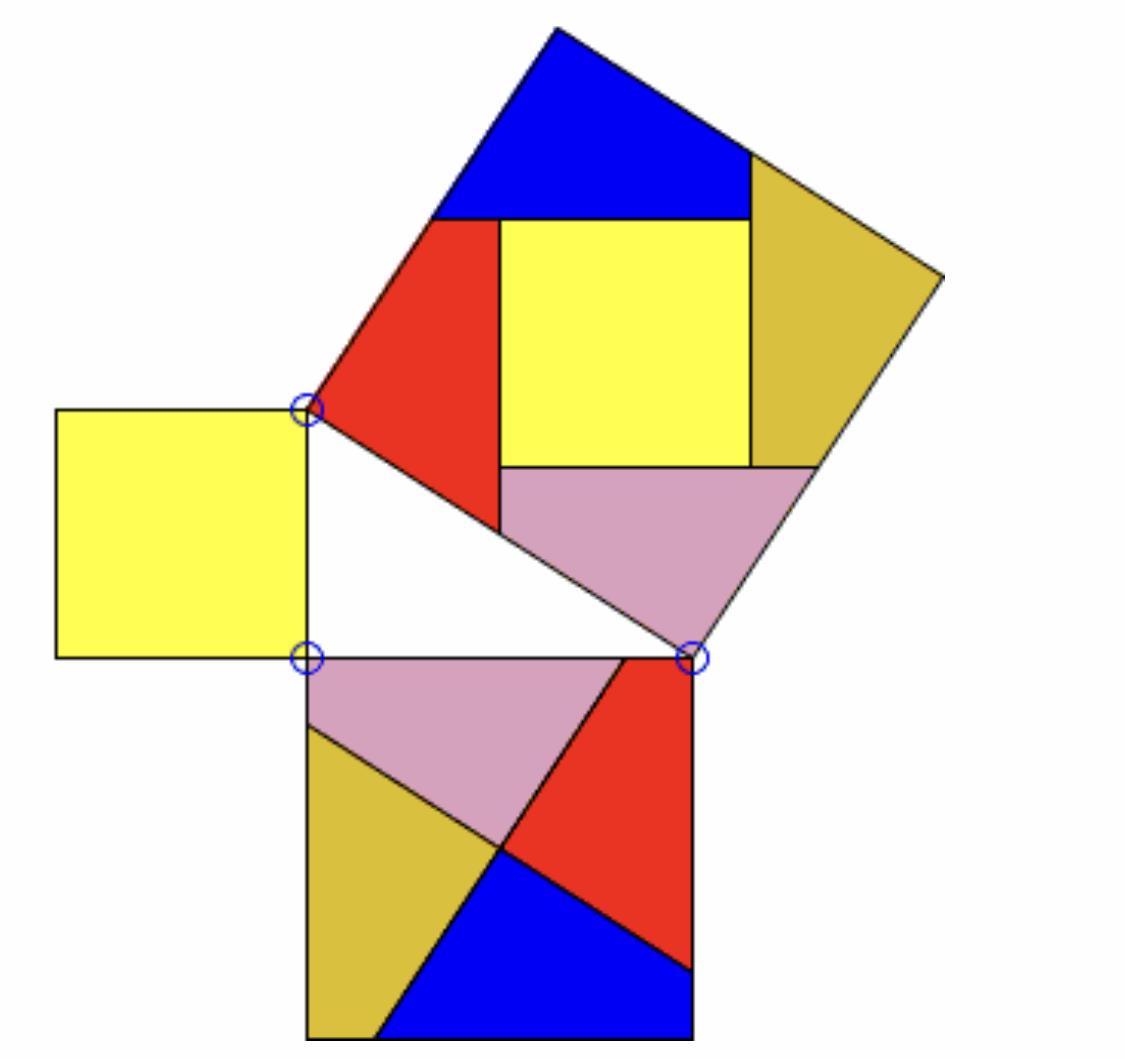
Cela constitue le théorème de Pythagore.
Vous souhaitez réaliser cette figure vous-même ? En savoir plus sur la façon de découper les motifs à l'intérieur des carrés pour les recoller ? On en parle ensemble ?
Une application du théorème de Pythagore
Cette propriété permet de calculer les distances dans un espace dit euclidien.
Si vous connaissez les coordonnées de deux points A et B, vous pouvez calculer la distance entre ces deux points en utilisant la formule :
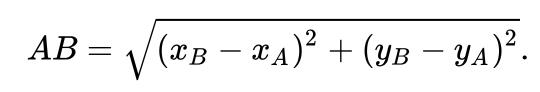
Cette formule provient précisément du théorème de Pythagore.
Le cas des triangles qui ne sont pas rectangles
Prenez un triangle ABC.
Si AB au carré est strictement supérieur à la somme des carrés des deux autres côtés, alors AB est le plus grand côté du triangle ABC, mais en plus, l'angle C est obtus, il mesure plus de 90 degrés.
Si AB au carré est strictement inférieur à la somme des carrés des deux autres côtés, alors l'angle C est aigu, il mesure moins de 90 degrés.
Le cas d'égalité correspond précisément à un triangle rectangle.
Comment savoir géométriquement qu'un triangle est rectangle ?
Prenez le côté le plus grand de ce triangle. Appelez-le C.
Appelez O le milieu de ce côté.
Tracez le cercle de centre O admettant le côté C pour diamètre.
Ce cercle passe par les deux sommets formant le côté C.
- Si ce cercle contient le troisième sommet du triangle obtenu, alors le triangle étudié est rectangle.
- Si ce cercle ne passe pas par le troisième sommet du triangle obtenu, alors le triangle étudié n'est pas rectangle.

